こんにちは、大学受験kawaiラボの河井です。期末テスト、終わってくる学校が出てきて問題を見たりしていますが、昨今平均的な子が解き終わることが物理的に不可能なテスト(70分で大問20個ある化学とか、50分で大問事実上10個ある物理とか)を作るのが流行りなのでしょうか、ちょっと作り手の粗さなり焦りなりが感じられるテストが増えてますね…。今日はそういう(ちょっとは言いたい)テストの愚痴の話ではなくて、テスト準備を見せてもらいながら感じた「問題/解答における文字や軸の設定」のお話です。なので数学にも通ずる話ですが、今日の素材は物理のお話です。
物理で投射運動の話をすると、だいたい下に書いたようなまとめにされていることが多いかと思います(タブレットで手書きだから下手なのは許して汗)。これらはそもそも等加速度運動の式v=v₀+at, x=v₀t+1/2at², v²-v₀²=2axの3式(もっと言えば3式目は2つの式からtを消去することで得られるのですが、まぁ便利なので)を小球の投げる状況ごとに適応したものでありますが、全暗記!と言われている人も多いことかと思います。
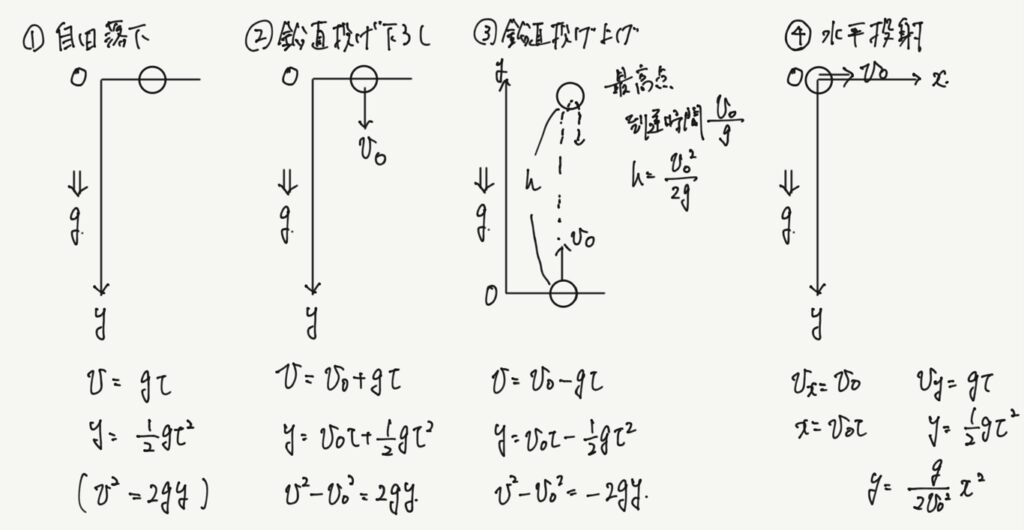
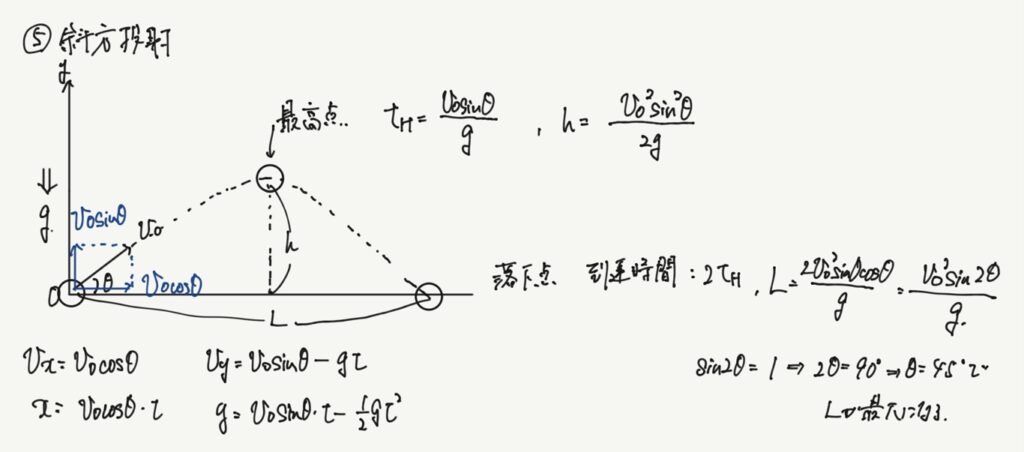
この公式の丸暗記でワークの基本問題は解けますし、高1の物理基礎で欠点を取ることはまぁ回避できますし、物理は取らないぞ、という人にはそれでとりあえず十分なのかもしれませんが、今後も物理とのお付き合いがあるとして、以下のような問題はどうでしょう?
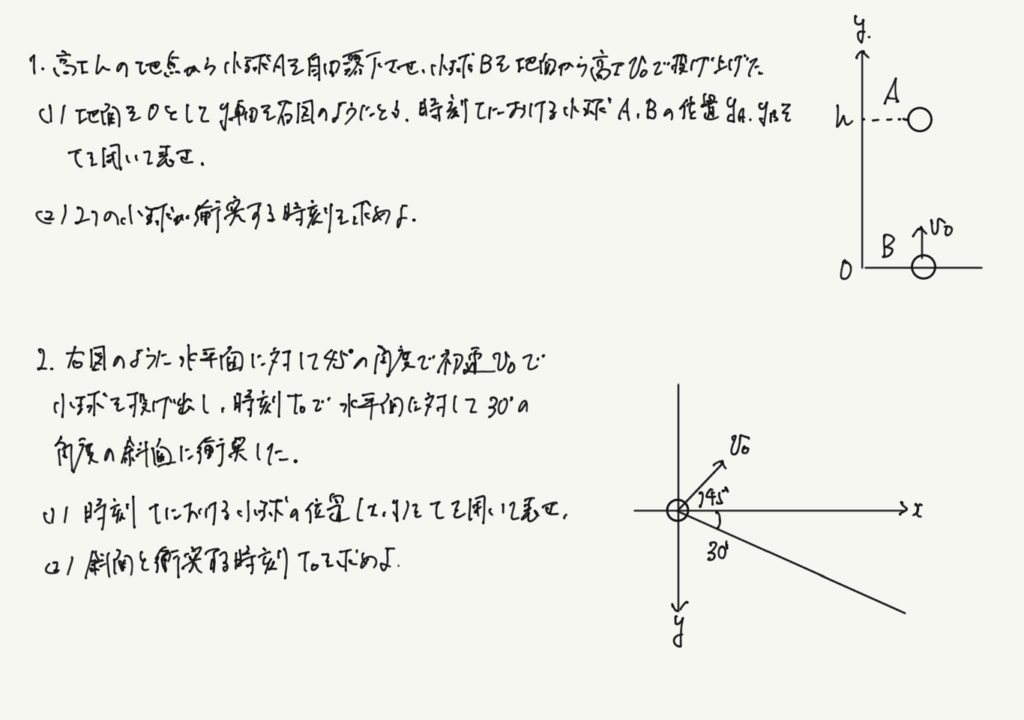
この問題、実は先ほどお見せした公式通りに立式しようとするとちょっと困ったことになってしまいます。1問目は小球Bにとってはこの座標設定は公式通りにできるのですが、Aについては公式と向きは逆だし、場所は0スタートじゃないし…、と修正が必要になるのです。2問目は斜方投射の向きとしては座標設定が逆向きで、あと斜面とぶつかるところをどのように表すか、という問題が生じてきます。公式の機械的な適用では早くもこの段階でうまくいかないことが現れてくるのです。
公式導出が重要、と言いますが、そもそもこれらの公式は最もシンプルな表現になるように、ある意味で「恣意的に」座標設定などを行なっているのです。つまり、人間が問題解決のために最も良い設定を使っているわけです。もし、問題解決のために必要であれば変えればいいものですし、また、上記問題1のように2つの物体で都合が食い違う場合にはどちらかに合わせる必要が出てきます。そういった「諸事情」(と僕はよく言っているのですが)まで含めて、丁寧に取り扱いを紹介しておく必要が指導者側にあるでしょうし、また、その練習をしっかり積んでもらうように促していかないといけませんね。
Leave a Reply