入試に出る？出ない？

こんにちは、大学受験kawaiラボの河井です。随分と暑くなってきました。今日は車を走らせていると温度が35 ºCを表示していて、これで6月上旬ですか…ととてもうんざりした気分になりますね。急な気候の変動は体調に影響しやすいので、皆さまお大事にお過ごしくださいませ。

さて、今日は少しこちらでも言及しましたが、「入試に出る・出ない」論議です。「ここはあんまり入試には出ないので…」と言われるアレです。なんでもできるに越したことはありません、はい、おしまい！では芸がないので、もう少し具体例も挙げながらお話ししていきたいと思います。

まず「入試に出る・出ない」という話にはテストというものの性格もあって、限られた出題数では全範囲の全ての事項を含められない、という前提があります。例えば大学受験の数学だと文理系など差異はありますがおおよそ3大問〜6大問になります。その中に全てを入れ込むのは不可能ごとであることをあらかじめご承知おき頂いて、以降の話を見て頂ければと思います。(薄く広く入れている共通テストでもいくつかの項目、例えばIIBの軌跡と領域や二項定理の話題は多くは見掛けられない、あたりでご納得頂ければ。)

その前提条件の上で「入試に出る・でない」という件についてコメントしている多くの人は入試の出題タイトル、例えば

第1問：微分法
第2問：確率
第3問：ベクトル
第4問：積分法
第5問：整数
第6問：複素数平面

みたいなものを見て、統計的に出る／出ないを言っている場合です。それって本当にそれでいいのか？ということです。例えば次の例題。

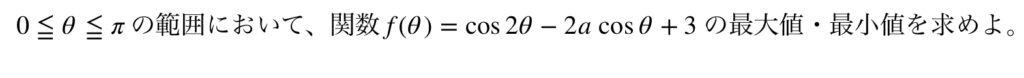
この問題、普通は「三角関数」とか「三角関数の最大・最小」とタイトル付けされます。ですが、置き換えを使うと数Iでやる2次関数の最大・最小問題の軸の位置による場合わけに帰着されます。ですが、問題タイトルには「2次関数」の言葉は出てきません。それをもって「2次関数は2次試験にはあまり出ないから」とは決して言うことができません。

それではもう1つ、よくある数IIの微分の問題。数IIIだと関数のところがややこしくなります。

これもよくある問題ですが、微分して求めた導関数f’(x)がx=1で0になるから、でaの値を求めて、それからそのaの値でちゃんとx=1で極大になるかを確かめる、という、定期テストのときにはテンプレのように解いている問題です。これ、気づいていただけたでしょうか？「そのaの値でちゃんとx=1で極大になるかを確かめる」というところ、単なるお作法にしてしまう人が多いのですが、x=1がf’(x)=0の解になるからでaを求めるのは必要条件であり、十分性を担保するためにそのaで条件を満たすことを確認するのです。これでようやく必要十分条件として答えとして提示することができます。数学の問題はよく「必要十分条件となる答えを求める」というような言い方をされます。多くの問題が答えに辿り着こうとするとその必要十分性を追求していることになりますが、いくつかの問題は値を出すところは必要性しかできておらず、十分性の保証が必要になります。これが数Iの集合と論理のところで学ぶ必要条件・十分条件の話が埋まっているところです。しかし、この問題のタイトルは「微分法」になるわけです。集合と論理の話を入試に出ないと言ってしまうような浅はかな発言をしてはならないわけです。

したがって、多くの大学で数学I・A(場合の数と確率、整数の性質)・II・B(数列・ベクトル)・III(理系のみ)と範囲設定していますが、その全範囲から出うるし、メインテーマや見た目が違っても他の単元の手法・知識・論理が埋まっていることは往々としてあります。そういった意味では「ここは入試にはあんまり出ないから…」と特に高2までに言うことは慎んだ方が良いでしょう。

その一方で、我々講師は「ここは入試にはあんまり出ないから…」という発言をそこそこします(ちゃぶ台返し)。その場合は過去問を精査して、受験までの残り時間と現状を勘案して、取捨選択の手段としてそのようにスパッと言い切り型にしていることがあります。共通テストとの兼ね合いから好んで数IIIの特に微積分が出題されることは事実、ほか、大学ごとに多少あれこれあるのですが、目標達成のための取捨選択のためにその辺をひとつひとつ精査した方策としてお伝えしていますので、それくらいのつもりで聞いて頂けるとありがたいです。